Home Tutors Exams

Euclidean-geometry

Written on
November 2019 - Paper 2

Question 8

$8.1$	In the diagram, $PQRS$ is a cyclic quadrilateral. Chord $RS$ is produced to $T$ . $K$ is a point on $RS$ and $W$ is a point on the circle such that $QRKW$ is a parallelogram. $PS$ and $QW$ intersect at $U$ . $P\hat ST=136^{\circ}$ and $\hat Q_1=100^{\circ}$ .

Determine, with reasons, the size of:
$\quad 8.1.1$	$\hat R$	$(2)$
$\quad 8.1.2$	$\hat P$	$(2)$
$\quad 8.1.3$	$P\hat QW$	$(3)$
$\quad 8.1.4$	$\hat U_2$	$(2)$
		$\textbf{[9]}$

Written on
November 2020 - Paper 2

Question 8.1

$8.1$	$O$ is the centre of the circle. $KOM$ bisects chord $LN$ and $M\hat NO=26^{\circ}$ . $K$ and $P$ are points on the circle with $N\hat KP=32^{\circ}$ . $OP$ is drawn.

$\:\: 8.1.1$	Determine, giving reasons, the size of:
$\quad (a)$	$\hat O_2$	$(2)$
$\quad (b)$	$\hat O_1$	$(4)$
$\:\: 8.1.2$	Prove, giving reasons, that $KN$ bisects $O\hat KP$ .	$(3)$
		$\textbf{[9]}$

Written on
November 2019 - Paper 2

Question 9

In the diagram, $O$ is the centre of the circle. $ST$ is a tangent to the circle at $T$ . $M$ and $P$ are points on the circle such that $TM=MP$ . $OT$ , $OP$ and $TP$ are drawn. Let $\hat O_1=x$ .

Prove, with reasons, that $S\hat TM=\frac{\displaystyle 1}{\displaystyle 4}x$ .		$\textbf{[7]}$

Written on
November 2020 - Paper 2

Question 9.2

$9.2$	Chord $QN$ bisects $M\hat NP$ and intersects chord $MP$ at $S$ . The tangent at $P$ meets $MN$ produced at $R$ such that $QN\parallel PR$ . Let $\hat P_1=x$ .

$\:\: 9.2.1$	Determine the following angles in terms of $x$ . Give reasons
$\quad (a)$	$\hat N_2$	$(2)$
$\quad (b)$	$\hat Q_2$	$(2)$
$\:\: 9.2.2$	Prove, giving reasons, that $\frac{\displaystyle MN}{\displaystyle NR}=\frac{\displaystyle MS}{\displaystyle SQ}$	$(6)$
		$\textbf{[10]}$

Written on
November 2020 - Paper 2

Question 10

In the diagram, a circle passes through $D$ , $B$ and $E$ . Diameter $ED$ of the circle is produced to $C$ and $AC$ is a tangent to the circle at $B$ . $M$ is a point on $DE$ such that $AM\perp DE$ . $AM$ and chord $BE$ intersect at $F$ .

$10.1$	Prove, giving reasons, that:
$\quad 10.1.1$	$FBDM$ is a cyclic quadrilateral	$(3)$
$\quad 10.1.2$	$\hat B_3=\hat F_1$	$(4)$
$\quad 10.1.3$	$\Delta CDB\,\|\|\|\,\Delta CBE$	$(3)$
$10.2$	If it is further given that $CD=2$ units and $DE=6$ units, calculate the length of:
$10.2.1$	$BC$	$(3)$
$10.2.2$	$DB$	$(4)$
		$\textbf{[17]}$

Written on
November 2019 - Paper 2

Question 10.2

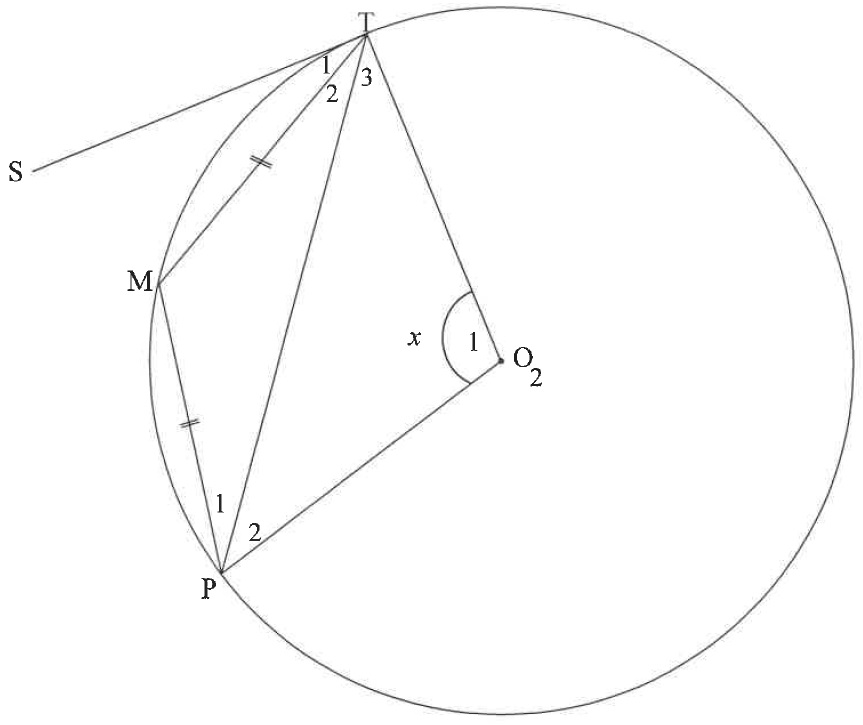
$10.2$	In the diagram, $ST$ and $VT$ are tangents to the circle at $S$ and $V$ respectively. $R$ is a point on the circle and $W$ is a point on chord $RS$ such that $WT$ is parallel to $RV$ . $SV$ and $WT$ are drawn. $WT$ intersects $SV$ at $K$ . Let $\hat S_2=x$ .

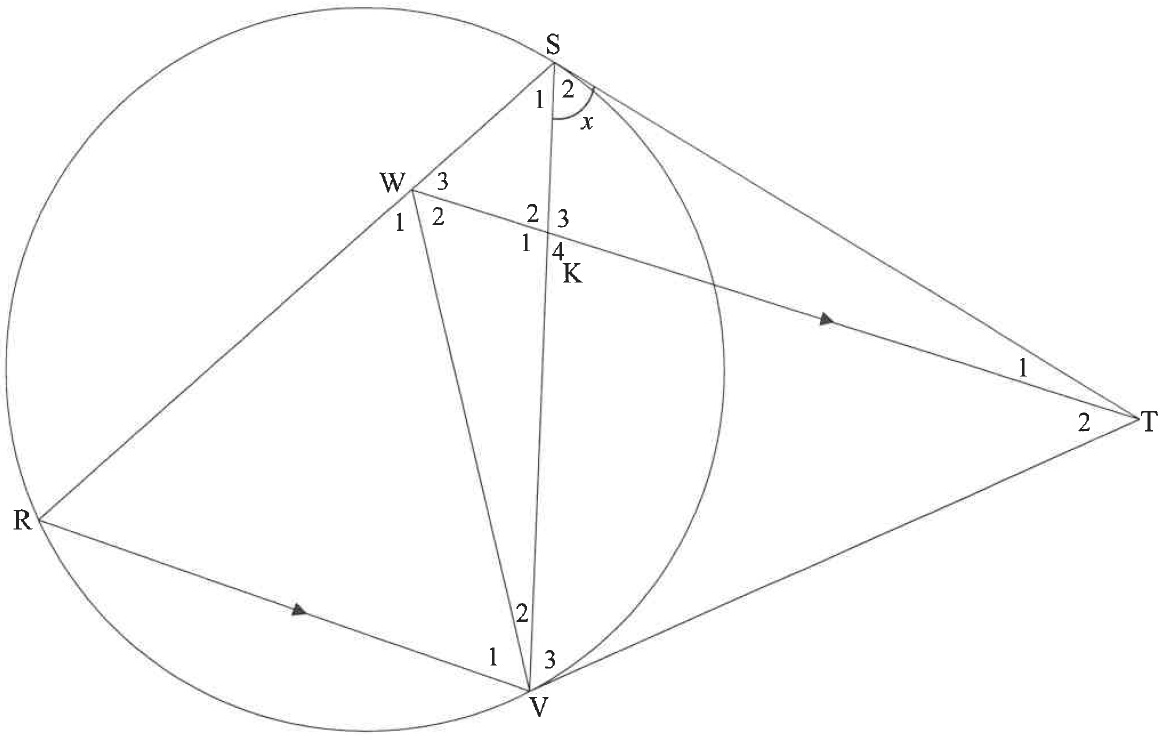$10.2.1$	Write down, with reasons, THREE other angles EACH equal to $x$ .	$(6)$
$10.2.2$	Prove, with reasons, that:
$\quad (a)$	$WSTV$ is a cyclic quadrilateral	$(2)$
$\quad (b)$	$\Delta WRV$ is isosceles	$(4)$
$\quad (c)$	$\Delta WRV\,\|\|\|\,\Delta TSV$	$(3)$
$\quad (d)$	$\frac{RV}{SR}=\frac{KV}{TS}$	$(4)$
		$\textbf{[19]}$

← Back to the exams